Головною особливістю Parik24 є його простота та доступність. Навіть новачок легко знайде цікаву для себе гру та зможе розпочати грати. Parik24 пропонує широкий вибір ігор – від класичних слотів до настільних розваг, включаючи ігри від провідних розробників, таких як Play’n GO.
Однією з головних переваг казино Parik24 є зручність. Вам не потрібно виходити з дому, щоб відчути азарт і хвилювання від гри. Все, що вам потрібно – це пристрій із підключенням до інтернету. Крім того, Parik24 приділяє особливу увагу безпеці гравців.
Усі транзакції захищені сучасними технологіями шифрування, тому гравці можуть бути впевнені в надійності та чесності казино. Для швидких та безпечних транзакцій використовуються банківські картки електронні гаманці.
Реєстрація в Parik24
У Parik24 реєстрація займає лише кілька хвилин. Перший крок до створення акаунта – перехід на офіційний сайт онлайн-казино Parik24. У верхній частині сторінки розташована кнопка «Реєстрація», яка допоможе вам швидко створити акаунт на Parik24.
Онлайн-казино Parik24 спрощує процес реєстрації для своїх гравців, роблячи його доступним та легким. Після реєстрації користувачі отримують доступ до ставки на спорт разом з іншими ігровими опціями.
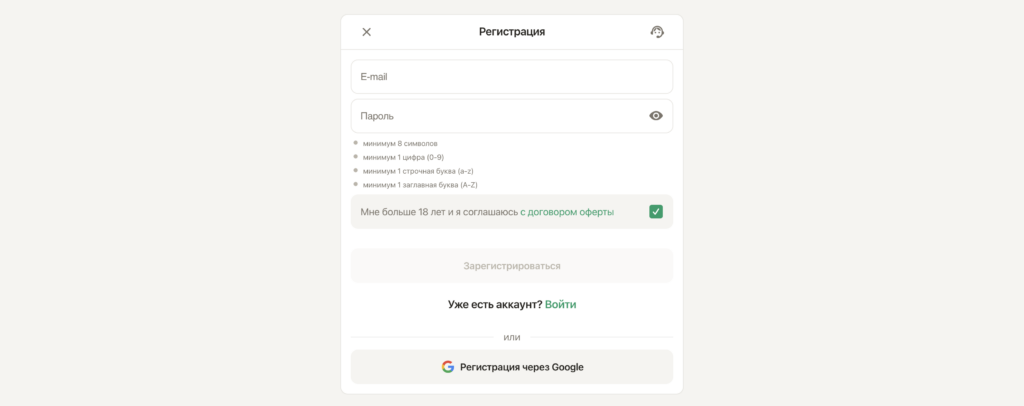
Для створення акаунта в Parik24 необхідно виконати кілька простих кроків. Перше та дуже важливе вимога – наявність дійсної електронної пошти та контактного номера телефону. Після введення цих даних ви будете перенаправлені на сторінку з реєстраційною формою. Parik24 вимагає лише базову інформацію від своїх гравців під час реєстрації, зокрема ваше ім’я, прізвище, контактні дані та іншу необхідну інформацію.
Під час реєстрації в онлайн-казино Parik24 важливо ретельно та точно заповнювати поля анкети. Переконайтеся, що правильно вказали свою електронну пошту та контактний номер телефону, оскільки вони використовуються для відновлення акаунта. Безсумнівно, Parik24 приділяє особливу увагу захисту персональних даних своїх користувачів і вживає всіх необхідних заходів для забезпечення їхньої безпеки.
Верифікація в Parik24
Parik24, як надійне та безпечне онлайн-казино, дотримується суворого процесу верифікації кожного акаунта. Верифікація в Parik24 необхідна для забезпечення безпеки та управління вашими рахунками. Це також допомагає підтримувати прозорість ігор та забезпечувати справедливість у грі.
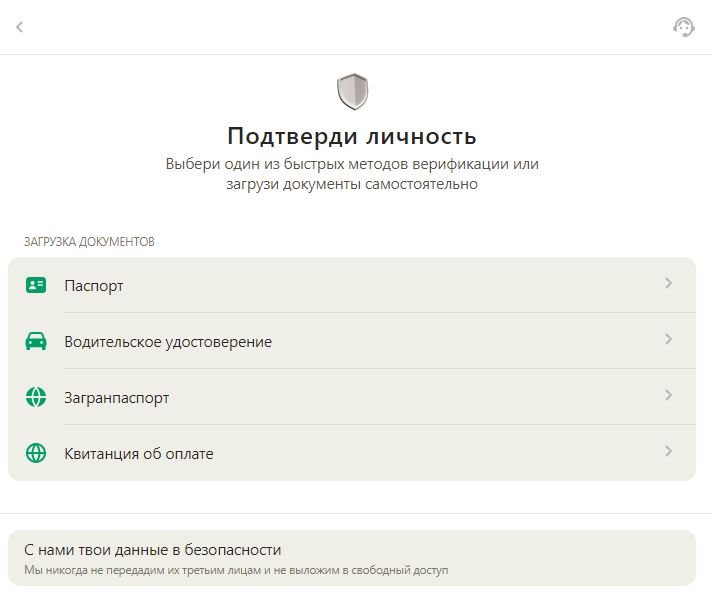
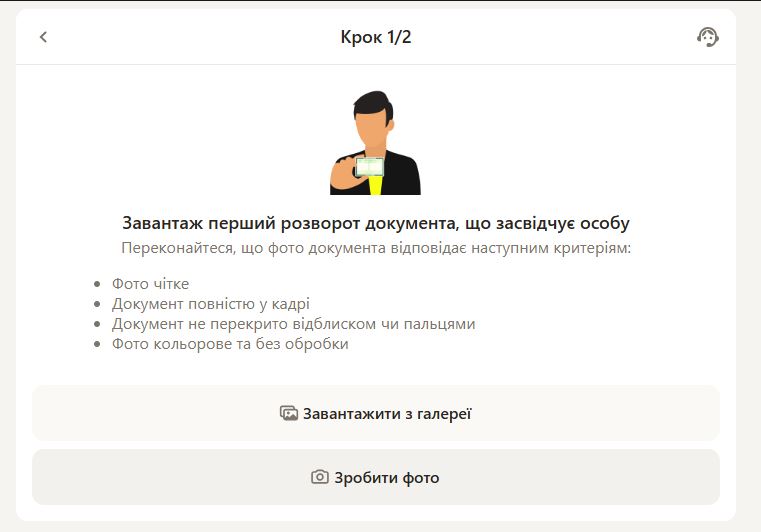
Які документи потрібні для верифікації в Parik24? Все просто: знадобиться документ, що засвідчує особу з фотографією, наприклад, паспорт або водійське посвідчення. У деяких випадках pari24 може вимагати підтвердження адреси, наприклад, рахунок за комунальні послуги. Усі надані документи повинні бути чіткими та добре видимими.
Верифікація в Parik24 зазвичай займає від кількох годин до кількох днів. Однак цей процес залежить від багатьох факторів і в окремих випадках може тривати до тижня. У будь-якому випадку, команда Parik24 робить усе можливе для пришвидшення цього процесу.
Процес верифікації в Parik24 є простим і зрозумілим: перший крок – це завантаження копії документа, що підтверджує особу, на онлайн-платформу Parik24. Після цього може знадобитися надання додаткових документів, таких як рахунки за послуги або банківські виписки.
Прийнятний список документів для верифікації в Parik24 включає, але не обмежується:
- Паспорт
- Водійське посвідчення
- Посвідчення особи
- Рахунки за комунальні послуги
На завершення, верифікація в Parik24 є ключовою частиною процесу створення акаунта та гри в безпечному і чесному середовищі. Parik24 прагне забезпечити зручність для своїх гравців і робить процес верифікації швидким та легким.
Способи входу на сайт Parik24
Для доступу до онлайн-казино Parik24 передбачено кілька зручних варіантів. Перш за все, ви можете зайти на сайт Parik24 через будь-який сучасний інтернет-браузер. Завдяки оптимізованому дизайну та швидкій реакції, вебсайт Parik24 забезпечує плавний та зручний ігровий досвід.
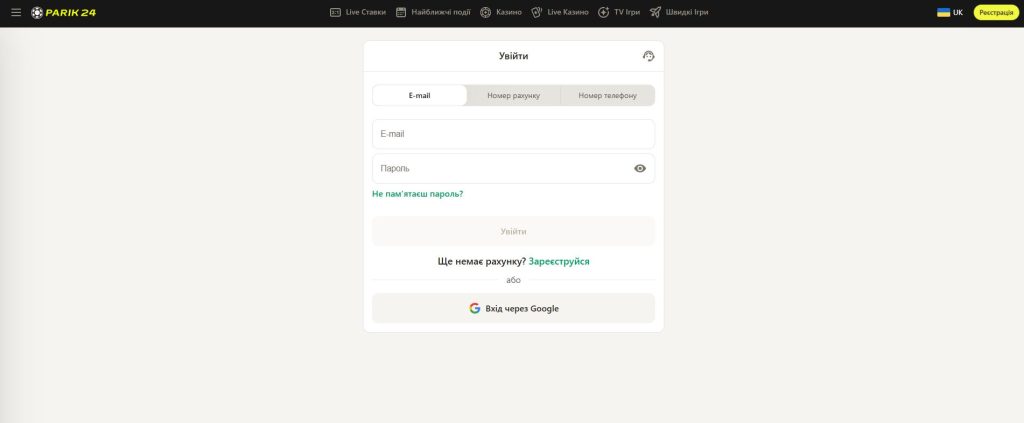
Перш за все, важливо відзначити, що мобільна версія сайту Parik24 адаптована до різних розмірів екранів і забезпечує повну функціональність порівняно з десктопною версією. Додатково, Parik24 пропонує мобільний додаток для зручності користувачів. Цей додаток Parik24, доступний як на Android, так і на iOS, забезпечує максимальну зручність та швидкий вхід до казино. Це дозволяє гравцям отримати доступ до своїх улюблених ігор у будь-який час і в будь-якому місці.
Розв’язання проблем з авторизацією Parik24
Якщо ви зіткнулися з проблемами під час авторизації в онлайн-казино Parik24, завжди є прості рішення. По-перше, переконайтеся, що ви правильно вводите свої облікові дані для входу в Parik24. Якщо проблема не вирішується, рекомендується звернутися до служби підтримки Parik24, яка працює 24/7 і завжди готова допомогти.
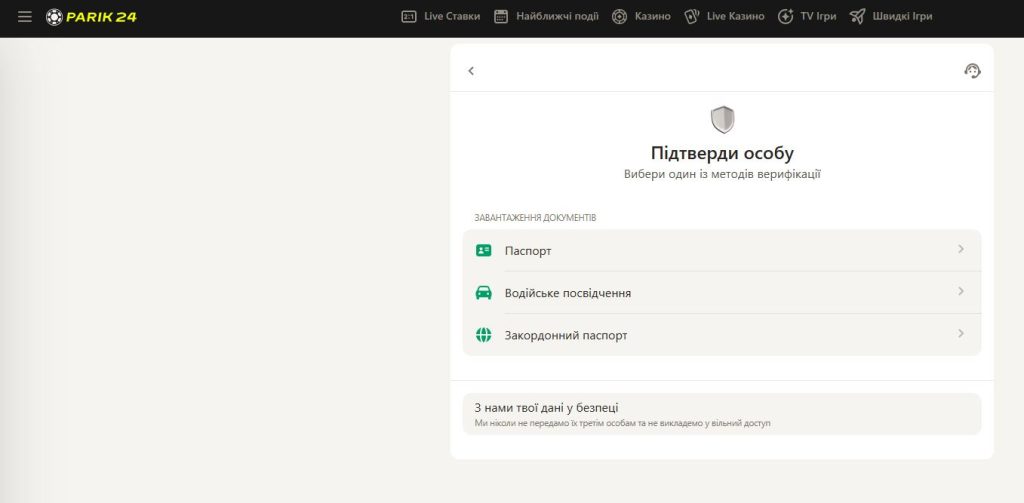
Якщо ви забули пароль від свого акаунта в Parik24, не варто хвилюватися. Відновлення пароля в Parik24 – це простий і швидкий процес. Перейдіть на сторінку входу та оберіть опцію «Забули пароль?». Вам потрібно буде ввести електронну пошту, вказану під час реєстрації акаунта. Протягом кількох хвилин ви отримаєте посилання для відновлення пароля від Parik24 на свою електронну пошту.
Дотримуйтеся інструкцій, надісланих вам на електронну пошту, щоб успішно відновити пароль та отримати доступ до свого акаунта в онлайн-казино Parik24. Якщо у вас виникнуть будь-які труднощі з відновленням пароля, зверніться до служби підтримки для допомоги.
Мобільний додаток Parik24
Мобільний додаток Parik24 – це ідеальне рішення для тих, хто любить насолоджуватися грою в онлайн-казино Parik24 у будь-який час і будь-де. Додаток Parik24 доступний для завантаження як на платформах Android, так і iOS, забезпечуючи швидкий та легкий доступ до улюблених ігор.
Parik24 з гордістю пропонує вам функціональний та зручний додаток. Особливості додатка включають повний доступ до ігор, можливість робити ставки в реальному часі, безперервний вхід у особистий кабінет та багато іншого. Використовуючи мобільний додаток Parik24, ви ніколи не пропустите можливість виграти.

Процес завантаження та встановлення додатка Parik24 максимально спрощений. Вам потрібно лише відвідати офіційний сайт Parik24, перейти в розділ «Завантажити додаток» та слідувати вказівкам. Якщо у вас виникнуть питання чи труднощі під час встановлення або використання додатка, фахівці служби підтримки завжди готові допомогти.
Як почати грати в Parik 24 mobile?
Почати грати в Parik 24 mobile дуже просто. Для цього потрібно виконати кілька кроків:
- Відвідайте офіційний сайт Parik 24: Перейдіть на офіційний сайт онлайн-казино Parik 24 за допомогою свого мобільного пристрою.
- Завантажте мобільну версію: Натисніть на кнопку “Завантажити мобільну версію” та завантажте додаток на свій пристрій.
- Зареєструйтеся або увійдіть в свій обліковий запис: Якщо у вас вже є акаунт, просто увійдіть. Якщо ні, зареєструйтеся, виконавши кілька простих кроків.
- Поповніть свій рахунок: Використовуйте банківські картки, електронні гаманці або інші доступні методи для поповнення рахунку.
- Виберіть свою улюблену гру: Після поповнення рахунку, виберіть гру, яка вам подобається, і почніть грати!
Мобільна версія Parik 24 забезпечує повний доступ до всіх функцій платформи, включаючи ставки на спорт, ігрові автомати та живе казино. Грайте в будь-який час і в будь-якому місці з Parik 24 mobile!
Мобільна версія сайту для доступ до ігор
Мобільна версія сайту Parik24 забезпечує зручний доступ до всіх ігор та функцій платформи з будь-якого мобільного пристрою. Завдяки адаптивному дизайну, мобільна версія автоматично підлаштовується під розмір екрану вашого смартфона або планшета, забезпечуючи комфортну гру без жодних обмежень.

Гравці можуть насолоджуватися улюбленими ігровими автоматами, робити ставки на спорт та брати участь у живих іграх, де б вони не знаходилися. Мобільна версія Parik24 підтримує всі функції десктопної версії, включаючи поповнення рахунку, виведення коштів та отримання бонусів. Це дозволяє гравцям залишатися в грі та не пропускати жодної можливості для виграшу.
Бонуси та акції Parik24
Parik24 пропонує своїм користувачам не лише якісні ігри та зручний додаток, а й привабливі бонуси та акції. Онлайн-казино Parik24 чудово знає, як здивувати своїх гравців і зробити їхній ігровий досвід ще приємнішим. В казино Parik24 ви знайдете різноманітні промоційні пропозиції та бонуси для нових і активних гравців, що робить гру ще більш захопливою.
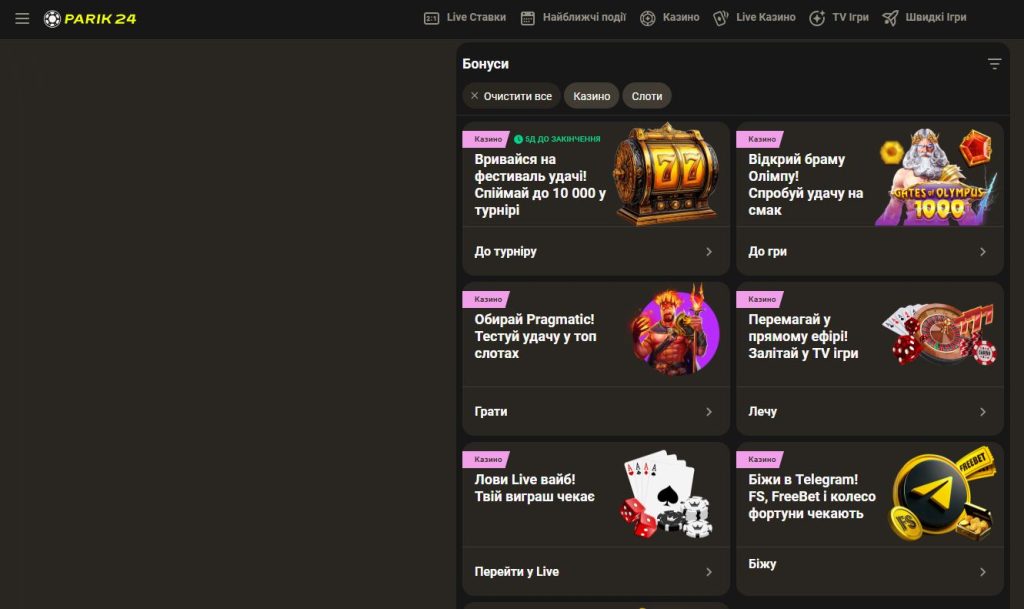
Parik24 вітає всіх нових гравців щедрим вітальним бонусом. Це особливий подарунок від казино Parik24, який допоможе вам розпочати свою подорож із приємною сумою на балансі. Ви будете приємно здивовані умовами відіграшу бонусів. Parik24 регулярно пропонує різні акції та програми лояльності, які допомагають вигравати ще більше.

Бонуси Parik24 – це шанс не лише збільшити свій баланс, а й отримати незабутні враження від гри. Вони доступні всім користувачам мобільного додатка Parik24 і готові принести вам задоволення та захопливі моменти. Не втратьте свій шанс стати частиною світу онлайн-розваг Parik24 і почніть грати вже сьогодні!
Вітальний пакет для нових гравців
Парік 24 пропонує привітальний пакет для нових гравців, який включає в себе бонуси та безкоштовні обертання. Після реєстрації на офіційному сайті онлайн-казино Parik24, нові гравці можуть отримати вітальний бонус у вигляді додаткових коштів на свій рахунок.

Це чудова можливість розпочати гру з вигідних умов та збільшити свої шанси на виграш. Крім того, нові гравці можуть отримати безкоштовні обертання в популярних слотах, що дозволяє ознайомитися з іграми без ризику для власних коштів. Вітальний пакет від Parik24 – це ваш перший крок до захопливого світу онлайн-казино.
Бонуси за запрошення друзів
Парік 24 пропонує бонуси за запрошення друзів, що робить гру ще більш вигідною та цікавою. Якщо ви запрошуєте своїх друзів приєднатися до казино Parik24, ви можете отримати бонуси у вигляді додаткових коштів на свій рахунок.
Це чудовий спосіб збільшити свій капітал та продовжити гру. Запрошуючи друзів, ви не лише ділитеся з ними захопливим досвідом гри в онлайн-казино, але й отримуєте додаткові переваги для себе. Бонуси за запрошення друзів – це ще один спосіб Parik24 зробити ваш ігровий досвід незабутнім.
Щотижневий кешбек
Парік 24 пропонує щотижневий кешбек для своїх гравців, що дозволяє повернути частину своїх втрат протягом тижня. Ця функція є чудовим способом зменшити свої втрати та продовжити гру. Щотижневий кешбек від Parik24 дозволяє гравцям отримати назад частину витрачених коштів, що робить гру менш ризикованою та більш приємною.
Завдяки кешбеку, ви можете насолоджуватися грою, знаючи, що частина ваших витрат буде повернена. Це ще один приклад того, як Parik24 піклується про своїх гравців та робить їхній ігровий досвід максимально комфортним.

100 безкоштовні обертання за поповнення рахунку
Парік 24 пропонує 100 безкоштовних обертань за поповнення рахунку, що є чудовою можливістю для гравців збільшити свої шанси на виграш. Якщо ви поповните свій рахунок на певну суму, ви можете отримати безкоштовні обертання в популярних слотах.
Це дозволяє гравцям насолоджуватися грою без додаткових витрат та збільшити свої шанси на виграш. Безкоштовні обертання – це чудовий спосіб ознайомитися з новими іграми та отримати додаткові виграші. Parik24 завжди прагне зробити гру для своїх гравців максимально вигідною та захопливою.
Ігрові автомати Parik24
Розпочніть свою подорож у світ великих виграшів із Parik24. Онлайн-казино Parik24 пропонує широкий вибір ігрових автоматів. Серед них ви знайдете як класичні слоти, так і сучасні ігрові автомати з тематичними бонусами та безкоштовними обертаннями. Parik24 ретельно відбирає кожен слот, щоб забезпечити максимальне задоволення від гри.
Parik24 співпрацює з провідними розробниками ігор, включаючи Pragmatic Play та Play’n GO, одного з лідерів у сфері популярних слотів. Їхні ігрові автомати відрізняються високою якістю графіки, унікальними бонусними раундами та оригінальними сюжетами. Кожен автомат на платформі Parik24 здатний задовольнити навіть найвибагливішого гравця.

На сайті Parik24 представлено широкий вибір популярних ігрових автоматів. Вони приваблюють гравців не лише яскравими та барвистими дизайнами, а й різноманітними функціями, які допомагають вигравати більше. Кожен слот в онлайн-казино Parik24 має свої особливості та переваги, тому гравці завжди зможуть знайти гру до смаку.

Розуміючи, наскільки важливо ознайомитися зі слотом перед грою на реальні гроші, Parik24 пропонує демо-режим. Ця функція дозволяє гравцям спробувати будь-який слот без ризику для свого балансу. Цей режим Parik24 ідеально підходить для новачків, які хочуть зрозуміти механіку гри, та для досвідчених гравців, які хочуть протестувати новий слот.
Популярні парік24 автомати серед українських гравців
Класичні слоти
Класичні слоти – це традиційні ігрові автомати, які створені на основі старих наземних слотів. Вони відрізняються своїми простими правилами та мінімальною кількістю ліній виплат. На сайті Парік24 можна знайти такі класичні слоти, як “Слот “Ромео і Джульєта”” та “Слот “Місіс Пай””. Ці слоти ідеальні для тих, хто хоче відчути класичний стиль гри. Вони пропонують гравцям простоту та ностальгію, що робить їх популярними серед шанувальників традиційних ігрових автоматів.
Відеослоти з бонусами
Відеослоти з бонусами – це сучасні ігрові автомати, які пропонують додаткові можливості виграшу. Вони відрізняються своїми цікавими сюжетами, якісною графікою та креативними бонусними функціями. На сайті Парік24 можна знайти такі відеослоти з бонусами, як “Слот “Гонки на швидкість”” та “Слот “Місія до Марса””. Ці слоти ідеальні для тих, хто хоче відчути захопливий досвід гри. Вони пропонують гравцям не лише можливість виграти, але й насолодитися захоплюючими історіями та інтерактивними бонусними раундами.
Джекпоти та прогресивні виплати в казино парік24
Парік 24 пропонує джекпоти та прогресивні виплати в своїх слотах, що дозволяє гравцям виграти великі суми коштів. Джекпоти – це особливі виграші, які можуть досягати значних сум, і вони доступні в багатьох ігрових автоматах на сайті Parik24.

Прогресивні виплати збільшуються з кожною зробленою ставкою, що робить гру ще більш захопливою та вигідною. Кожен гравець має шанс виграти великий джекпот, що додає додатковий рівень азарту та інтриги до гри. Parik24 пропонує своїм гравцям найкращі можливості для великих виграшів, роблячи їхній ігровий досвід незабутнім.
Живе казино
Живе казино Парік 24 – це інтерактивний формат, який дозволяє гравцям взаємодіяти з реальними дилерами в режимі реального часу. На сайті Парік 24 висока якість стрімінгу та чітке зображення, що дозволяє гравцям відчути себе як у справжньому наземному казино.

Популярність live-ігор на Парік 24 стрімко зростає серед українських гравців. Завдяки живому казино, ви можете насолоджуватися такими іграми, як блекджек, рулетка та баккара, не виходячи з дому. Це чудова можливість відчути справжній азарт та атмосферу казино, залишаючись у комфорті свого дому.
Особливості live-ігор на сайті парік24 ua
Live-ігри на сайті Парік 24 ua відрізняються високою якістю стрімінгу та чітким зображенням, що дозволяє гравцям відчути себе як у справжньому наземному казино. На сайті Парік 24 ua представлені такі популярні ігри, як рулетка, блекджек та покер, які проводяться реальними дилерами в режимі реального часу.

Гравці можуть спілкуватися не лише з дилером, а й з іншими гравцями за столом, що додає додатковий рівень соціальної взаємодії та азарту. Завдяки live-ігор на сайті Парік 24 ua, ви можете насолоджуватися атмосферою справжнього казино, не виходячи з дому.
Crash-ігри та інші інноваційні розваги в живе казино

Crash-ігри – це новий тип ігор, які пропонують швидкий та захопливий досвід гри. Вони відрізняються своїми простими правилами та швидким темпом гри. На сайті Парік24 можна знайти такі crash-ігри, як “Crash” та “Aviator”. Крім того, на сайті можна знайти інші інноваційні розваги, такі як живе казино з реальними дилерами. Це ідеальний варіант для тих, хто хоче відчути справжній досвід гри в казино. Живе казино Парік24 дозволяє гравцям взаємодіяти з реальними дилерами та іншими гравцями, що додає додатковий рівень реалізму та азарту до гри.
Фінансові операції
Фінансові операції у Парік 24 казино здійснюються швидко та безпечно. Користувачі можуть скористатися банківськими картками Visa та Mastercard для швидких і безпечних транзакцій. Електронні гаманці такі як Skrill і Neteller також доступні на платформі Парік 24, що забезпечує додаткову зручність для гравців.

Крім того, підтримуються криптовалютні платежі Bitcoin та USDT, що дозволяє здійснювати фінансові операції з максимальною швидкістю та безпекою. Всі методи розрахунків забезпечують швидкість та безпеку фінансових операцій, що робить процес поповнення рахунку та виведення коштів максимально комфортним для користувачів.
Депозит та поповнення рахунку на Парік24 Ukraine
Депозит та поповнення рахунку на Парік24 Ukraine є простим і швидким процесом, що дозволяє гравцям миттєво почати грати. Мінімальна сума депозиту становить лише 200 гривень, що робить гру доступною для всіх. Максимальні суми можуть варіюватися залежно від обраного платіжного методу.

Поповнення балансу відбувається миттєво, а комісії за внесення депозиту, як правило, відсутні. Гравці можуть скористатися банківськими картками Visa та Mastercard, електронними гаманцями Skrill та Neteller, а також криптовалютними платежами Bitcoin та USDT. Це забезпечує максимальну зручність та безпеку фінансових операцій на платформі Парік24 Ukraine.
Надійність та легальність
Парік 24 відзначається своєю надійністю завдяки наявності ліцензії, виданої Комісією з регулювання азартних ігор та лотерей України. Ця ліцензія підтверджує легальність роботи Парік 24 online та забезпечує відповідність всім стандартам безпеки та чесної гри.

Гравці можуть бути впевнені, що їхні дані та фінансові операції захищені, а ігровий процес є справедливим та прозорим. Ліцензія також гарантує, що Парік 24 дотримується всіх необхідних регуляторних вимог, що робить його надійним вибором для гравців.
Ліцензія в казино Парік 24
Казино Парік 24 має ліцензію, видану Комісією з регулювання азартних ігор та лотерей України. Ця ліцензія підтверджує легальність роботи казино і гарантує відповідність всім стандартам безпеки та чесної гри.
Ліцензія забезпечує захист даних гравців і гарантує прозорі фінансові операції. Гравці можуть бути впевнені, що їхні особисті дані та кошти знаходяться під надійним захистом. Казино Парік 24 дотримується всіх необхідних регуляторних вимог, що робить його надійним вибором для гравців, які шукають безпечне та чесне онлайн казино.
Захист і безпека даних для гравців
Казино Парік 24 дуже серйозно ставиться до захисту даних гравців. Для цього використовуються найсучасніші методи захисту даних, такі як SSL-шифрування і протоколи безпеки. Це гарантує, що всі транзакції та особисті дані гравців захищені від несанкціонованого доступу.
Крім того, казино Парік 24 має спеціальну службу підтримки, яка завжди готова допомогти гравцям у разі виникнення технічних труднощів або питань щодо безпеки даних. Гравці можуть бути впевнені, що їхні дані знаходяться під надійним захистом, а ігровий процес є безпечним та чесним.
Парік 24 прагне забезпечити максимальний рівень безпеки для своїх гравців, щоб вони могли насолоджуватися грою без жодних турбот.
Підтримка клієнтів
Парік 24 пропонує високоякісну службу підтримки, яка доступна 24/7. Команда професіоналів завжди готова допомогти у разі виникнення технічних труднощів або питань щодо використання платформи.

Гравці можуть зв’язатися з представниками служби через електронну пошту або онлайн-чат, що забезпечує швидке та ефективне вирішення будь-яких проблем. Служба підтримки Парік 24 завжди готова допомогти гравцям у разі виникнення питань або проблем, забезпечуючи високий рівень обслуговування та задоволення користувачів.
FAQ
Як швидко відбувається виведення коштів для гравців в парік24?
Всі запити на виведення коштів обробляються протягом декількох годин. Точний термін залежить від обраного способу та підтвердження особи користувача.
Чи є доступ до мобільної версії сайту для гравців на сайті парік24?
Так, мобільна версія повністю адаптована для комфортної гри з будь-якого пристрою, забезпечуючи зручний доступ до всіх функцій платформи.
Як зареєструватися на сайті парік24 для нових гравців?
Реєстрація займає всього кілька хвилин. Достатньо натиснути кнопку “Зареєструватися”, вказати електронну пошту, придумати пароль і підтвердити реєстрацію.
Чи можна отримати доступ до бонусів для гравців після виведення коштів?
Так, навіть після виведення коштів гравці можуть брати участь в акціях та отримувати бонуси, якщо вони відповідають умовам програми лояльності.
Чи потрібно зареєструватися на сайті, щоб отримати доступ до демоверсій ігор?
Ні, для доступу до демоверсій ігор на сайті не потрібна реєстрація. Ви можете спробувати грати безкоштовно, але для реальних ставок реєстрація обов’язкова.
